The Look Elsewhere Effect
Today we explore the games statistical context can play with your mind.
Statistics is a hard subject. Evidence based decision making hinges on our ability to understand the evidence. Human intuition often conflicts with statistical reality. Our goal today is to show you how counter intuitive statistics can be, and how context can affect your expectations.
Our aim is to discuss a phenomena crucial to understanding why so much excitement around potential discoveries in Particle Physics fluctuates as more data is collected, and why that’s actually a good thing. But first, we review a classic, mind bending statistical problem.
The Monty Hall Problem
The Monty Hall Problem is famously frustrating to folks without a strong background in statistics. For whatever reason, it’s mildly counterintuitive.
It’s even more frustrating to explain it, but here we go!
Imagine a pile of cash sitting on a table behind a closed door. Your job, as a contenstant, is to pick that money hiding door from among three identical doors. Behind the other two doors are goats.
“Not a bad game!” you might say. “A one in three chance of winning a pile of cash! That’s way better than the lottery!” You pick door number two.
For dramatic effect, the game progresses. The host opens one of the wrong doors for you, revealing a goat. Now there are two doors. And a question:
“Do you want to keep the door you picked, or do you want to switch doors?”
What do you do?
To a statistician, the answer is obvious. Instantaneously obvious. To everyone else, they’re faced with a dilemma.
Perhaps there’s some human psychology around the fact that you’ve already selected a door. That it’s your door. But the technical odds are clear: You can increase your chance of winning by 33% if you switch doors!
And this is where people get hung up.
“No that’s crazy.” They say, “There are only two doors now. The odds should be 50/50!”
This is the wrong refrain we hear time and again while explaining this problem. If you’re in that camp, don’t fret! Many people struggle with this problem.
To better understand the solution, let’s raise the stakes a bit. Let’s consider a generalization of this problem that I first heard from Seth Godin.
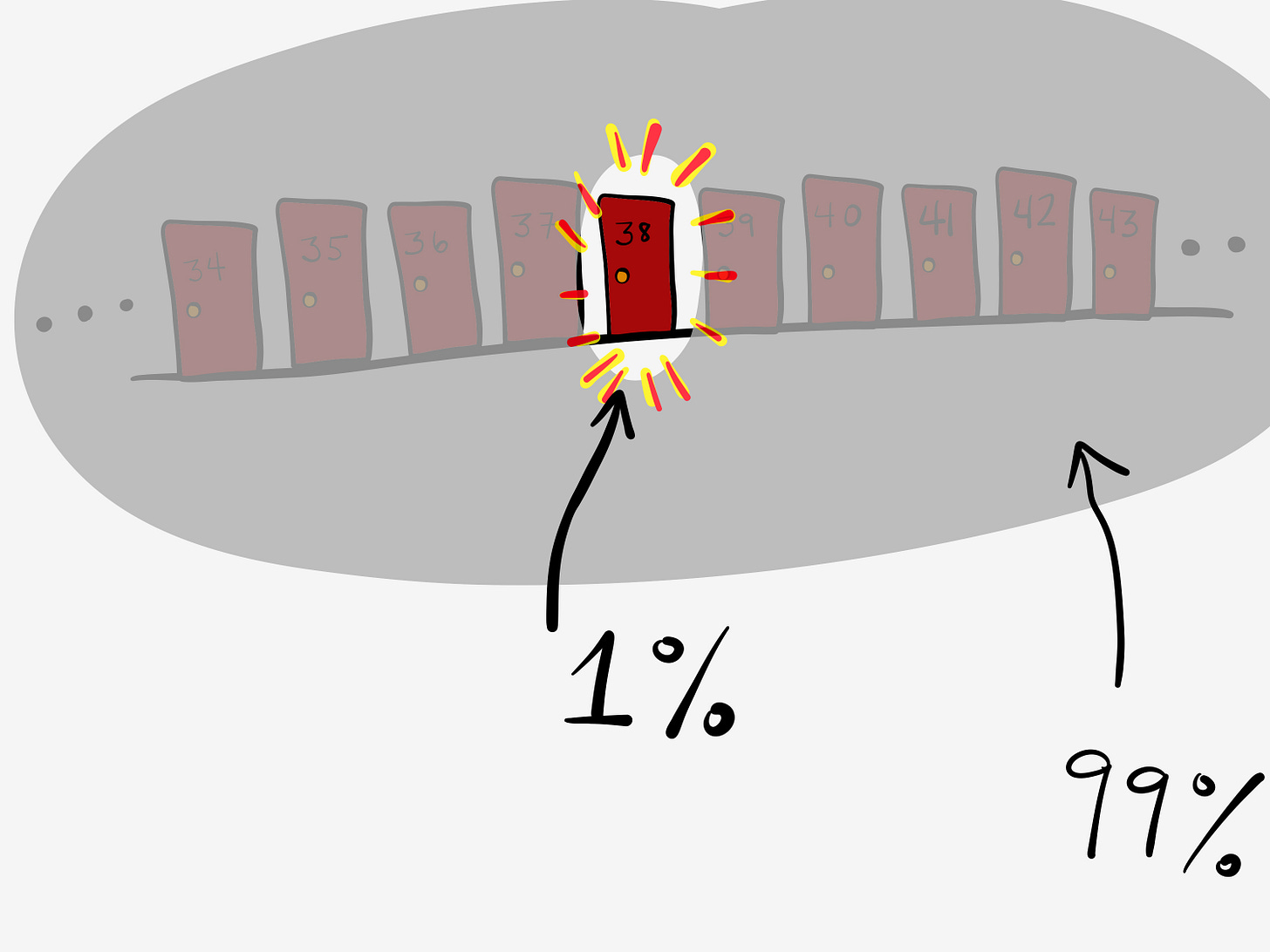
Instead of three doors, suppose there are 100. Behind one door is that pile of cash. That gives you a 1 percent change of being right. Behind every other door is a goat. You pick your door, and then one by one, the host opens one of the “wrong” doors, revealing a goat.
When it comes down to the last couple of doors, do you say to yourself?
“Wow! I picked one of the last doors! I did a real good job!”
No. I mean you might, but you’d be delusional. They’re not opening your door on purpose. Obviously, that’s the point of the game. The conflict. The drama. The host is going to force you to make a choice in the end, when there are two doors left standing. Yours. And whatever one is left standing.
Do you switch your door?
And this is where it gets really frustrating for both the student and the instructor. Because most of those “It’s 50/50!” folks are still lodged in the “it’s 50/50” mindset. There are only two doors left. The one you picked, and the one left over.
But let’s be clear. If you switch doors, you have a 99% chance of winning that pile of cash. If you don’t, it’s a 99% chance of greeting a goat.
“But that’s a stupid game! They’d never go for that!” The 50/50 camp will often reply. Right. Obviously. That’s why on TV there were only three doors. This is an exaggerated example. I understand you’re frustrated, so let’s go over it one more time:
You made a choice. You picked 1 out of 100 doors. Let’s say door number 38. That’s a 1 percent chance of winning the cash. That’s what you know. But you also know something else. You know that there are exactly 99 goats out there. So when the host - Monty Hall - shows you 98 goats, should you be surprised? No. You know there’s 98 goats. There should be one more! He hasn’t shown you anything new. Or has he?
You know there is a pile of cash behind one door. The chance of being right with door 48 is 1 percent. Another way to say that is your chance of being wrong is 99%. That means that there is a 99% chance that the pile of cash is behind a door not labeled 48.
Then the doors begin to open. It’s not door 1, 2,3,4,5,6,7,8,9,10,12, 13,14,15…all the way to 100. So which is it, door 11 or door 38?
99 percent of the time, it will be the other door, door 11.
You should switch your door. Read this again if you’re not convinced.
What if there are no piles of cash?
I suspect that part of the trouble with understanding the Monty Hall Problem is that there is no answer that guarantees you the cash. Human perception tends to distort probabilities, particularly when they’re mixed up with risk and reward. The 100-door version of the problem aims to account for this, but there’s still a chance you can lose by switching doors. I also suspect that’s where the frustration emerges. A 50/50 split removes the sense of agency from the problem, but a 99/1 split suggests fault.
Particle physicists face something of an analogous problem when looking for new, elementary particles. Often there is a wide range of possible masses for such discoveries. That mass range might range from one GeV - the approximate mass of the proton - to hundreds of GeV.
When trying to fit models to data, you have to pick a specific value of the mass. To effectively scan over the whole range, you might agree to do 100 evenly spaced values. This effectively cuts that large mass range up into “bins”, and you can perform your analysis with that value representative of that bin. We are simplifying this procedure a lot, but conceptually you can think of those bins as doors. Doors in the extended Monty Hall Problem.
As you go through your analysis, you start opening those doors. And you find some goats. Those are the doors where a new particle of that mass just does not fit the data.
But when you have a lot of bins, there’s often a few that might be able to support such a particle. Your analysis in some bins might show some hints of new physics. They might deviate from the predictions of the Standard Model by two, three or more standard deviations. This could be big news! Behind such a door might be a pile of cash indeed: The Nobel Prize!
Or there might be nothing.
This is what makes the statistical problem even harder: in particle physics, unlike the Monty Hall problem, you don’t know for certain if there’s a pile of cash behind any door. They might all be goats!
A Different Game
Let’s revisit the Monty Hall problem, but with a subtle shift to the rules. Let’s say that each door has a 1 in 3 probability of revealing a pile of money. But individually.
This way, we can play with one door. If you open the door, there is a 33.3% chance of finding the money. Otherwise there’s a goat. But one door is boring.
Let’s suppose there are three identical doors. Each door - individually - has a 33.3% percent chance of giving you some money. You pick a door, say door number 1.
Monty Hall then opens door number 3. To his relief, it’s a goat.
Then he asks: “Do you want to switch doors or stay with the one you’ve got?”
In this case, you do you. Changing doors won’t change your chances. Each door has a 33% chance of giving you a pile of money. Much better than the lottery, right?
Now let’s go to the 100 door game, and see how our subtle rule shift can begin to play tricks on your mind.
You are now confronted with 100 identical doors, each with an individual chance of giving you a pile of cash. But you can only pick one. So you do. You pick door 48.
Now Monty starts opening all the doors, one by one. Door 1, A goat. Door 2, A goat. Door 3, A goat. This goes on and on. Somehow, miraculously, Monty opens 98 doors and they were all goats. This is a rare event, statistically speaking. On average, we’d all expect there to be 33 piles of cash.
But there aren’t. There are 98 goats. And two doors. Door 11, and door 48.
Monty then asks. “Do you want to keep your door, or switch?”
Does it matter? What do you do?
The Psychology of Coin Flips
This second 100-door scenario feels vaguely like another problem. Let’s say you flip a coin 99 times and, miraculously, each time it lands on tails.
Assuming it’s a fair coin, what are the chances the coin lands on tails again? On heads?
It’s 50/50.
But it doesn’t feel that way does it?
You might call such a phenomena what it is. A winning streak. Or a tails streak. Flip a coin 10 times, how many streaks will you find? Finding heads twice in a row might not be so unexpected. But 3 times in a row starts to feel uncomfortable. Four times in a row and you might check the coin.
But what if you flip the coin 1000 times? Would a five-in-a-row streak feel that unusual? But what about a 99-in-a-row streak?
The uncomfortable truth is, all of this is possible, but the probability that the coin lands on heads for each flip is 50%. A five-in-a-row streak happens just over 6% of the time1. It’s fairly uncommon.
But what if you clip the coin 1000 times? You might expect a few events that have a 6 percent chance of happening. In fact, you might expect quite a few of them!
Such streaks are often called statistical fluctuations. While it is true that in statistics we expect the average to converge when we do a large number of experiments - in this case to 50% - what also can scale with the the number of those experiments are the size of those fluctuations2.
The Look Elsewhere Effect
When particle physicists are doing their analyses - when they’re looking for a new particles - they’ll have to pick a specific mass for model consistency. To scan over a large possible mass range - a large region of available parameter space - they’ll typically run the same analysis a large number of times, one for each tiny mass bin.
Particle physics obeys the laws of Quantum Mechanics, which is inherently probabilistic. Additionally, there is also always going to be random experimental error.
In most analyses- from some of those mass bins - the data will show nothing abnormal. They’ll be totally consistent with the presence of nothing new. These are the goats.
But owing to chance, the data in a few of those bins might just be a little off. The particles that were observed might tack a little too closely to one side. Or perhaps some rare particles just happen to be present more often than they would normally be. These data might be hinting at the presence of a new particle! A pile of cash!
Or they might just be goats: statistical fluctuations.
As the collider takes more and more data, those over abundant, rare particles might just thin out in events from that mass range. The probability of finding a new particle in that bin - in other words - will decrease with more data.
Because particle physicists often have to scan over large ranges of parameter space, statistical fluctuations are a part of their job. This apparent rise in potential discoveries as a function of scanning a large range of possibilities is sometimes called the Look Elsewhere Effect.
So how do Scientists stay sane in light of so many false positives?
Two things: First, put a really high threshold for discovery. Particle physics has set an arbitrary rule at 5-standard deviations from the null result - that’s about 1 in 3.5 million type of fluctuation.
Second, you rescale the significance of your potential discovery by an amount proportional to the size of the total mass range you investigated3. That’s a quick, ad hoc rule for including the fact that you ended up looking at so many doors before settling on one get at might give you pile of cash.
In practice of course the details are much more intricate. The CMS experiment has a great primer for students interested in the Look Elsewhere Effect phenomena.
A Difference of Expectations
Experimentalists are always throwing the cold water of statistical skepticism. Many theorists are rabid to chase down potential signals for discovery.
The one thing that makes the practice of particle physics different from either of our two Monty Hall games is that nobody knows what the probability of finding that pile of cash is beforehand. Nobody knows if there is a particle waiting to be discovered behind any of the doors.
Theorists may have a particle bias - or expectations - for particular mass ranges based on the models they’ve studied or created. They may have a very good reason to expect there to be particles.
I was trained as a theorist. The difference in epistemic approach to particle physics that experimentalists had felt very foreign to me. I’m only now coming close to feeling like I understand their perspective.
We were trained to think in terms of Lagrangians and coupling constants. They were trained to think in terms of analyses and resonance widths. Our expectations were sharply piqued around models like minimal supergravity.
Experimental expectations always felt more uniform, and that they were more willing to consider less appealing models if it meant they could scan a different region of parameter space.
The two combined - reckless optimism and due diligence - have been a good balance for progress in particle physics
That said, theorists - at least some of those who that taught me - where full of unbridled optimism as the LHC turned its attention beyond the Higgs boson.
But that wave broke hard on the physical reality that persists today: nothing new has been discovered. My advisor cautioned me that progress would be necessary slow. And discussions with him eventually revealed to me another kind of “look elsewhere effect”: physicists have been looking for Weak Scale Supersymmetry for a long time.
Here we’ve allowed both a “heads” streak and a “tails” streak. To flip all heads five times in a row would have the probability: 0.5 x 0.5 x 0.5 x 0.5 x 0.5 = 0.0315, or 3.125%.
Some of this is odds based, you have more chances to earn a streak, but some of this is structural. You can’t have a 10-streak when you only flip a coin 5 times.