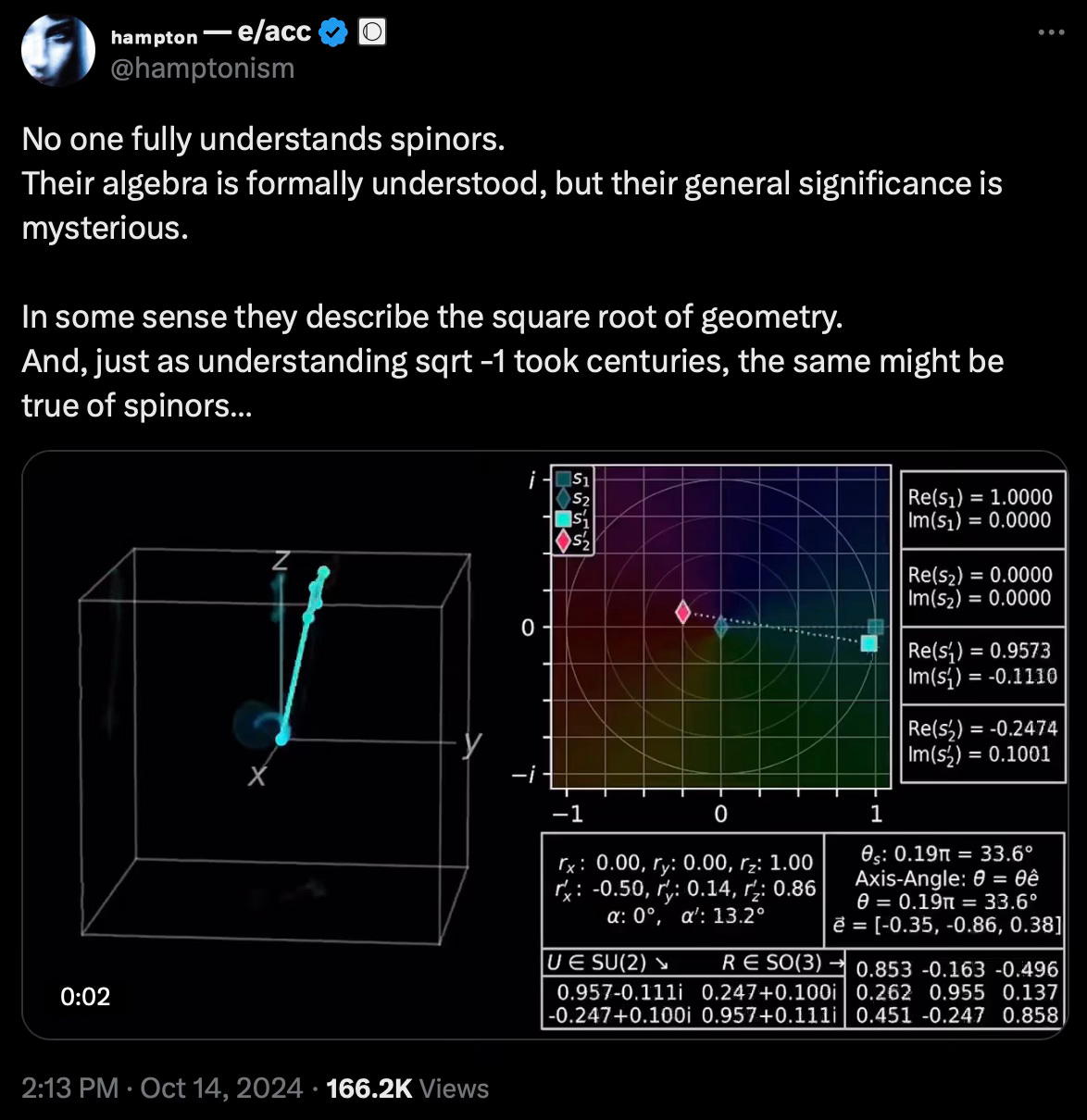
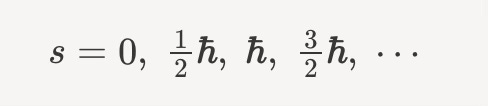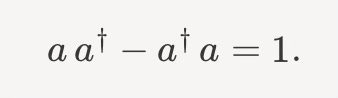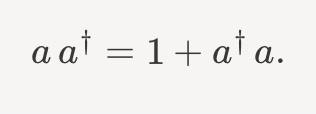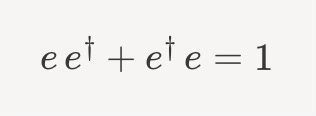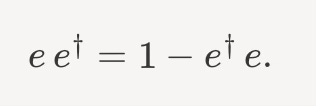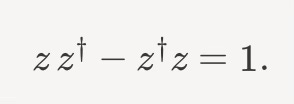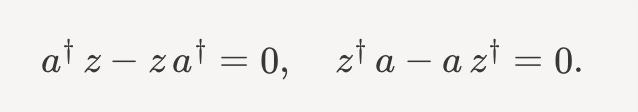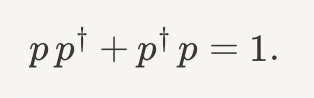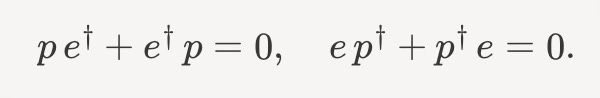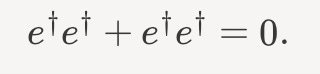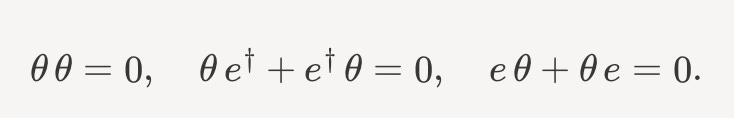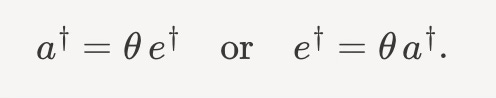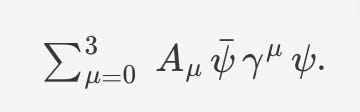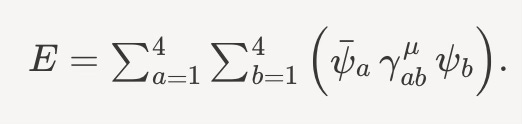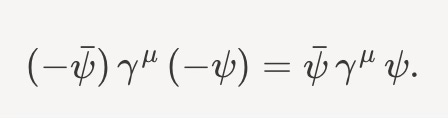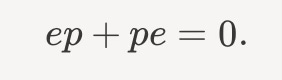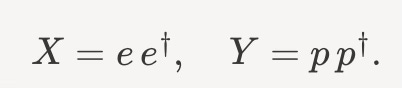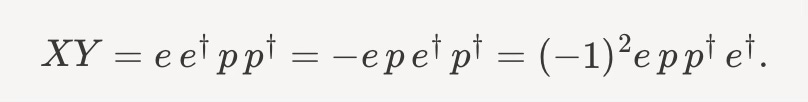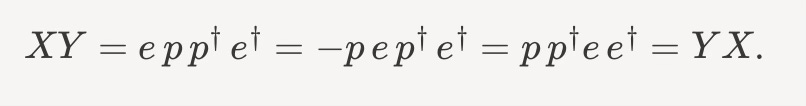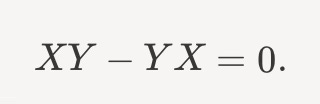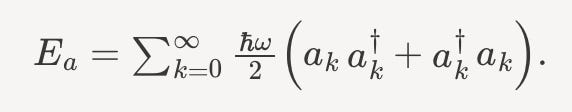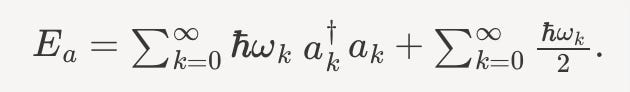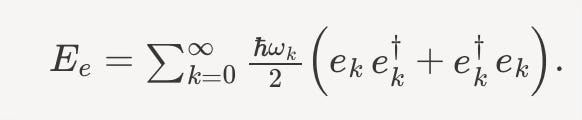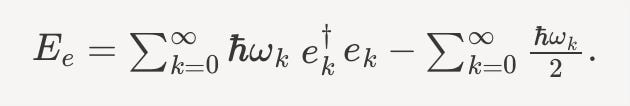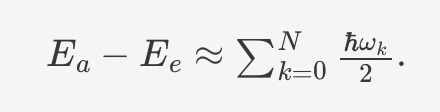A few months ago I stumbled upon a pretty wild tweet.
Spinors are a kind of vector, a special kind of vector. They are structurally more primitive than the usual vectors we use to describe the position and velocity of objects in elementary physics. They are also more difficult to explain.
But spinors are not mysterious. At least not to everyone.
It’s all about encoding information. Python is a simple programing language, but C is more primitive. You can ask Python and C to do the same things, but C is closer to the “silicon” carrying the actual electrons around. Pointers are probably just as mysterious to a Python developer as a spinor is to a student of linear algebra.
The tweet above reads more like a prayer than a logical argument. Our aim today is get you up to speed on spinors, and hopefully convince you that this tweet is inane.
First, “No one fully understands spinors” is vacuous. We’ve already spoken about that at length:
Second, spinors “describe the square root of geometry” in much the same way that “motorcycles” describe the “square root of cars”. But before we get in to any of that, where the hell does a tweet like that even come from?
Down the Rabbit Hole
The melodramatic saga of what might be called post-Twitter has turned up a lot of e/acc, STEM “enthusists” who share countless anecdotes but appear to be out of their technical depth1. This account was new to me, but the video graphic felt too well-produced for some random account. It had to come from some other source.
Sure enough, it was a screen capture of a YouTube video by Richard Behiel2, a metrology engineer with an emphasis on computational materials science. In that video, Behiel apparently used the “nobody understands” proposition as a narrative tool to engage viewers in a serious discussion of their mathematical properties.
To be clear, his video was an informative technical discussion with some unfortunate, philosophical trimming. Specifically, Behiel’s narrative attempted to veil the Spin-Statistics Theorem in a shroud of “nobody understands” mystery.
Mysticism is a strange stance to take for an educator, so I engaged him directly in the comments.
Okay, so Duck and Sudarshan. Deeper we go.
Ian Duck was a nuclear physicist at Rice University. EC George Sudarshan3 was a theoretical physicist at UT Austin. Together they authored a few works on the Spin Statistics Theorem, including the text that Behiel referred to in his comment4.
These authors were looking to solve an aesthetic problem5. The Spin Statistics Theorem as proved by, for example, Wightman and others was too technical and abstruse.
The Spin Statistics Theorem assigns of algebraic properties to particles6 based on what effective representation of the symmetries of spacetime they fall into. Spinors are the mathematical representation that are assigned to fermions like the electron. These should be contrasted with vectors that form representations that model force carrying particles like the photon, the gluon or the W and Z bosons7.
In Quantum Mechanics, such assignments lead to drastically different physical properties. Notably, the Pauli Exclusion Principle allows atoms to form what understand macroscopically as matter. The collective phenomena of bosons that include lasers, superconductors and superfluids.
Aesthetic problems of course are not problems of Science. They aim to solve propositions of value. Proponents of the aesthetic will only be satisfied when they say they are sufficiently satisfied8. Duck and Sudarshan’s final proof involved positing the physicality of Grassmann algebras and rotational invariance.
From the conclusion of their work,
“What remains to be understood in more fundamental terms is the existence of the two types of oscillator: number valued and grassman valued.
Finally we are forced to conclude that although the Spin-Statistics Theorem is simply stated, it is by no means simply understood or simply proved.”
Duck and Sudarshan, Am.J.Phys. 66 (1998) 284
What’s unfortunate about their discussion is that the “existence of two types of oscillator” is pretty intuitive to anyone who has studied supersymmetry9.
Supersymmetry
Supersymmetry is a continuous symmetry that relates representations of rotation groups. Minkowski space - the four-dimensional stage where the physics of Special Relativity plays out - is supersymmetric.
Just as x, y and z are related by rotational symmetry of R^3, bosons and fermions are related by a continuous transformation loosely referred to as a supersymmetry. Unlike rotations, we don’t exactly have an intuition for what the latter means, physically10.
Because our models of physics play out in Minkowski space, individual particles must fall into representations of the symmetries enjoyed by Minkowski space. Mathematically, this statement implies that each particle we observe must come with some intrinsic angular momentum. We call this spin. The allowed values of angular momentum are half integral units of a fundamental constant, ℏ
By definition, bosons have integral units of ℏ. Fermions have half-integral units. The Spin Statistics Theorem tells us that bosons and fermions have distinct algebraic properties. The main implication - the one that vexed hamptonism-e/acc, Behiel, Duck and Sudarshan so - is the so-called Pauli Exclusion Principle.
The Pauli Exclusion principle asserts that identical fermions cannot coexist in the same place at the same time. They may not have the same physical state. This is fortunate for us because electrons are fermions, and electrons are restricted to specific orbitals around the atomic nucleus. This affords us the very structure of matter as we know it11.
Bosons, by contrast, are allowed to exist in the same physical state. Photons are bosons, and this is a big part of the idea behind lasers12.
To see how bosons and fermions can be related, it helps to dig a little deeper into their algebraic properties.
Creation and Annihilation Operators
In Quantum Field Theory, particles aren’t fundamental but can be created and destroyed as part of any physical process.
For example, an electron may pass by another election, and one may admit a photon, while the other one absorbs it. In this case the photon is created and then destroyed. This is our low-level model for how the electrostatic repulsion of two electrically charged particles works
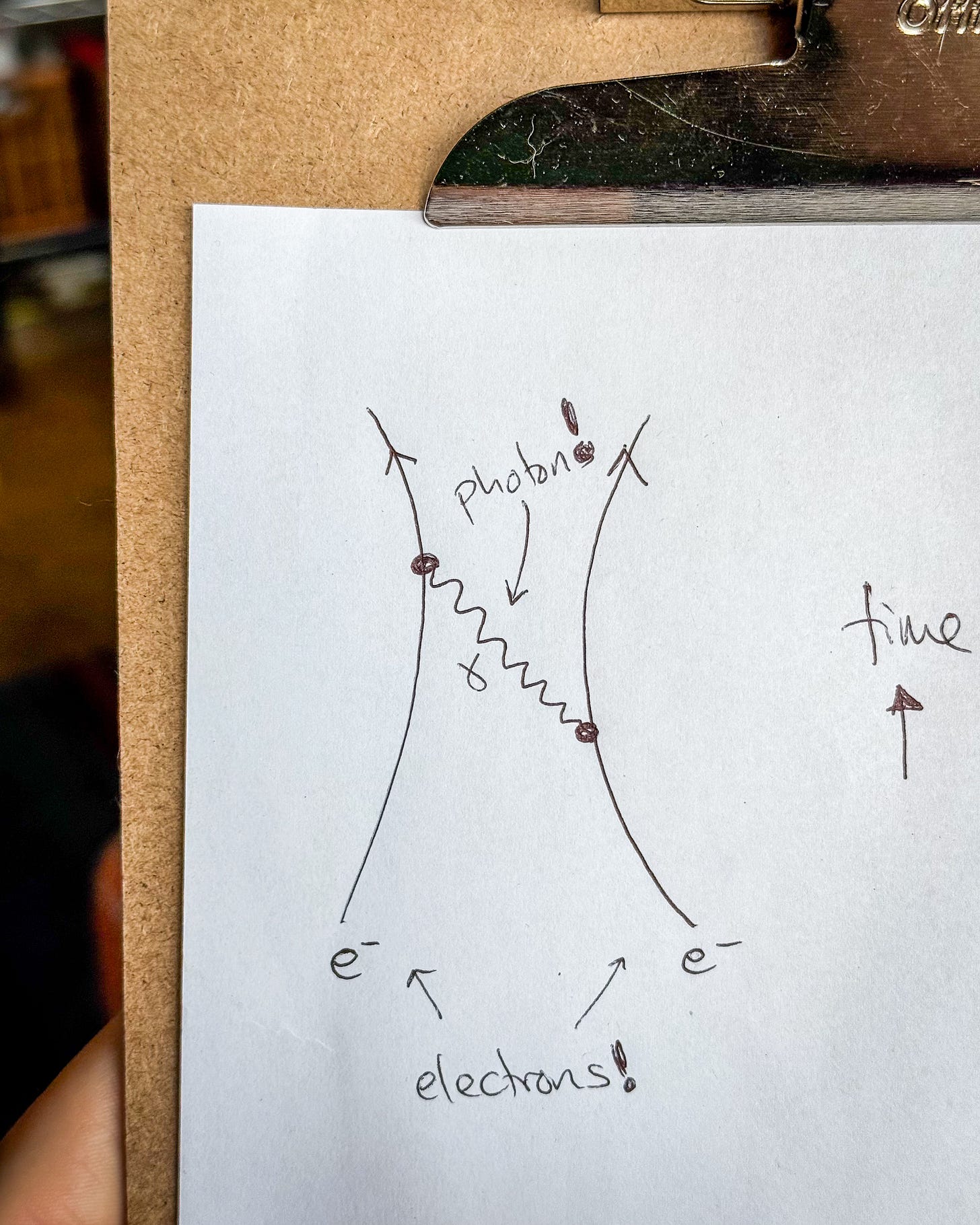
Fermions can be created and destroyed as well. For a more nuanced example, a photon may temporarily disappear, converting into an electron-positron pair which recombines into a photon shortly thereafter. This induces a small correction to the strength of the electromagnetic force between two such electrons
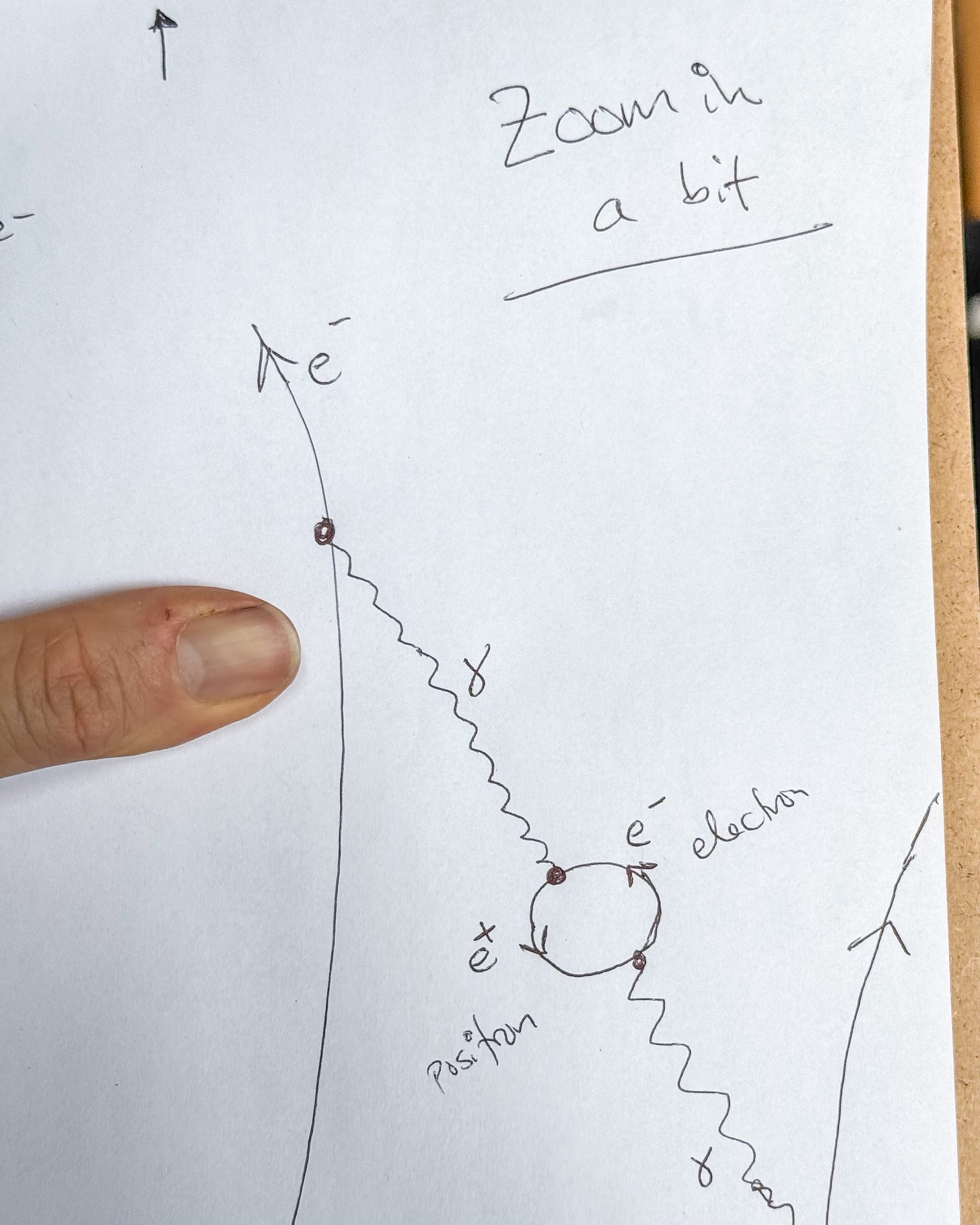
Mathematically we represent this phenomena with particle creation and annihilation operators. For a boson, a† creates a particle, and a annihilates it. For a fermion, let’s write these as e† and e, respectively13.
These symbols enjoy their own algebra relationships. For the boson, we have
One way to understand that relation is to say, suppose we have 5 photons around. If we create one, a†, then we’ll have 6. If we then annihilate one, we’ll back to 5. So you can think of aa† as the creation of a single new particle, followed by its immediate annihilation. Whereas, a†a first annihilates one, bringing you down to 4 photons, and then creates one, bringing you back to 5.
So, numerically, we say that the first case gives us one extra temporary photon to play with,
But interpretation gets tricky with fermions. Their creation and annihilation operators satisfy a different rule,
What’s important to keep in mind with fermions is the Pauli Exclusion Principle. You are only allowed to have 0 or 1 electron present in the same state. So we have
If we start in a state with zero electrons, then e†e doesn’t make any sense. You can’t annihilate an electron that doesn’t exist. So it counts as a zero So ee† gives us - for a brief moment anyway - a single electron. Good.
Similarly, if we had s single electron, e†e would first annihilate it, then recreate it. So the right hand side of this equation is consistent with temporarily having zero electrons. Of course, by the Pauli exclusion principle, we cannot create second electron, so ee† on the left-hand side would also have to give zero.
The Origin of Antisymmetry
Of course, this logic only works for particles that are identical. We are assuming that a and a† represent the same kind of particle. They both represent photons. But suppose instead that we want to know about a photon and the Z-boson.
The latter would have it’s own version of creation and annihilation operators, let’s call them z† and z, respectively. We would then have, as with the photon,
But it probably doesn’t surprise you that the photon and the boson don’t care about each other, algebraically. In particular,
Mathematically, we saw that the a and z operators commute. We don’t care which happens first, creation or annhilation of distinct particles. Quantum Mechanics doesn’t care because it’s easy to tell them apart. They are not identical. They arise from different quantum fields.
What’s absolutely wild about fermions is that the minus sign difference remains true. If p represented the proton - another kind of fermion - then we’d of course have
But now, it’s as if protons and electrons care about each other’s existence somehow
Mathematically, we say that fermionic operators are naturally anti-commuting. Incidentally, this is precisely how we understand the Pauli exclusion principle, as
Which can only be true if e†e† = 0. Put differently, what makes fermions weird is that e† doesn’t equal zero, but e†e† does.
A Symmetry between operators
Supersymmetry relates the operators a and a† with e and e†. Schematically, it rotates one into the other. One way to think about that is to take some auxiliary fermionic variable θ, where
We can then say that either
Notice that because θθ = 0, we have to pick one. This symmetry only works one way.
It should be said here that we are being extremely schematic, emphasizing only the even/odd duality between bosonic (vector) and fermionic (spinor) representations.
This variable θ, plays the same role as the cosine of the rotation angle between coordinates in the x,y and z plane. θ rotates between the vector and spinor representations of the group of isometries of Minkowski spacetime.
Supersymmetry then asserts that the bosons, created by operators a† are essentially the same particle as the fermions, created by e†, they just have different spin angular momentum when measured14.
Two to One
If you take everything we’ve said seriously up to this point, it appears that fermionic representations - the spinors - are more fundamental than the bosonic ones, the vectors. However, it is important to remember that this is a mathematical statement, not a physical one. In particular, it is not the case that a fundamental, vector boson - like the gluon - is somehow “composed” of two fermions.
Nevertheless, it is true that a pair of fermions can combine in ways that resembles the behavior of a vector boson. This brings us to perhaps a better way to understand the relationship between spinors and vectors.
When is a Vector a Vector? When is it a spinor?
For simplicity, let’s restrict to the familiar case of three-dimensional vectors in three-dimensional space, R^3.
Yes, as a vector space R^3 is a collection of all arrays of three-distinct numbers. It can also be thought of as a target for the action of 3 x 3-matrices, the linear transformations on R^3.
Certain subsets of these matrices can also form an algebraic group. The set of all rotations in three-dimensional space form a very important group in physics - the special orthogonal group. In this case we sometimes say that R^3 is a representation for that group, SO(3). Confusingly, sometimes it’s called the vector representation of SO(3).
The group SO(3) also has a spinor representation. Amusingly, a spinor representation of rotations in three-dimensions can be explicitly written as a two-dimensional array of complex numbers. We’re written a bit about them a while back when studying the Stern-Gerlach experiment
Understanding why the spinor representation is so different from the standard, vector representation requires a bit of technical study. It’s like switching from Python to C. That’s a more specialized topic than we have room for today, but we’ll consider it soon enough.
Bringing Spinors and Vectors Together
The interaction term between two electrons and a photon can be written as
Here A is the photon, and ψ is the electron15.
This interaction term can be thought of as the inner product between two vectors, the photon’s A, and the electron-positron combination, E,
The E in turn is actually the inner product of two spinors, with a matrix16 γ smashed between them,
Note that it is just a happy accident that in four-dimensions spinors are also four-component objects. In three-dimensions, as already discussed, they are two-component objects.
What’s important here is that rotations in the spinor representation are not the same as those in the vector representation. When we rotate the spinor ψ to -ψ, that is, if rotate it by 180 degrees, then what happens to the vector E?
Nothing. It’s the same
Generally, if I rotate it through an angle φ, the vector E will rotate by 2φ.
Formally, rotations in the space of spinors are only half of what they are in the space of vectors.
This is similar to the observation that two reflections comprise a rotation. But this is formally different. A rotation of a spinor is not a reflection for a vector.
Another way to see this is to consider pairs of fermionic operators.
Earlier we saw the annihilation operators for electrons and protons anti-commute:
Let us instead build some composite operators,
We can then compute
Continuing,
Hence
And so, in this sense, the commutation relations for bosons from the Spin Statistics theorem follow from the anti-commutation relations of the fermions.
It’s still “Supersymmetry, Stupid”
Supersymmetry may not be explicitly realized in our real world, but this doesn’t change the fact that it exists, mathematically.
Supersymmetry gives us an immediate explanation to Duck and Sudarshan’s aesthetic complaint as to why fermionic operators anticommute. Fermions - represented by spinors - are a more fundamental way of encoding information about rotational symmetry of Minkowski space.
We needed to jump intellectually from Quantum Mechanics to Quantum Field Theory to understand the existence of identical particles that gave rise to the Spin-Statistics Theorem. Similarly, we need to jump to supersymmetric Quantum Field Theory to understand the origin of the fermionic operators, writ large.
This is not a comment on how nature treats supersymmetry. It’s merely a question of mathematical machinery.
To close, I’ll give you one more example of how supersymmetry tends to clear up the structure of Quantum Field Theory.
The Vacuum Energy
The energy of a scalar field in Quantum Field Theory can be written in terms of the creation and annihilation operators as,
Applying the algebraic relation above, we find,
The last term should bother you. It represents the vacuum energy. The vacuum energy is a known and measurable effect. That sum is infinite.
One aesthetically pleasing thing about supersymmetry comes when looking at the same energy computation for a fermion,
in this case,
Here we find the same problem, only the vacuum energy is negative.
Supersymmetry implies that the individual energies of the different modes of the fields ω_k are the same. Hence the total vacuum energy of a supersymmetric particle, that should include both its fermion and boson pieces, vanishes identically.
What if Nature is Supersymmetric?
It’s possible that supersymmetry is broken, much in the same way that the electroweak symmetry is broken by the Higgs mechanism. There was a lot of hope that these two phenomena were related after the Higgs was discovered at the LHC. I wrote about this a few years ago:
Do we really need new particle physics?
Thomas Kuhn’s The Structure of Scientific Revolutions has made the “paradigm shift” into a trope for scientific progress. While this model of change certainly fits in retrospect, anticipating the next paradigm shift is not a well-defined problem. But this doesn’t stop folks from trying.
If supersymmetry is realized but broken, that means there is an energy scale above which nature is supersymmetric. For example, if we can get the center-of-mass energy of collisions between particles up above that energy - perhaps 20-100 TeV - we might be able to see new particles like a photino17 emerge.
To a rough approximation, then the vacuum energy of such a scenario would be the difference
Which would have made for a nice, intellectual story.
TL;DR
Spinors are cool.
Some old Scientists were concerned that the Spin Statistics Theorem was too abstruse to understand. They know about spinors, but weren’t sure why they had to introduce anticommuting operators for fermions. They took it as an uncomfortable axiom. The then wrote a book about all this and that book started confusing people.
Fermions are modeled by spinors, which are a more primitive construction than vectors. Within this construction emerges the concept of supersymmetry, which relates vector and spinor representations.
Supersymmetry may not be realized explicitly by nature, but it does exist as a mathematical property. It imposes a natural explanation for why operators representing fermions and being modeled by spinors, must have anticommutation relations.
More on spinors soon.
Aside from the usual crackpots, this includes accounts like Physics Memes, Physics In History, and so on. This post in some sense is a response to their near constant supply of random equations and unhinged anecdotes.
Behiel’s YouTube channel laudably aims at bringing theoretical physics to the masses. Behiel himself appears to be learning the material as he posts it, more evidence that teaching is a useful method for learning.
Sudarshan was an interesting fellow who also had a direct hand in the study of coherent states in quantum optics. We will be talking directly about these coherent states in our technical blog this week:
A more concise treatment was given in an article that may still be available on UT’s website. There is also a summary in a sweet, humanizing poem written by Duck for the occasion of Sudarshan’s 75th birthday.
The aesthetic problem with the proof was put forward as a question from physicist Dwight Neuenschwander in a 1994 issue of the American Journal of Physics.
Or quantum state combinations of such particles, like the “Cooper Pairs” Behiel refers to in his response. His complaint about visualizing such pairs is understandable, as the BCS theory of superconductivity pairs two electrons (fermions) into a single “Cooper Pair” (boson) by physical momentum, not by physical location.
Vector particles have intrinsic angular momentum valued as integers times some fundamental unit, ℏ. Spinors have half-integral units of ℏ. Scalar particles - those in the simplest possible representation, have zero intrinsic angular momentum, and qualify - per the spin statistics theorem - as bosons as well. (Zero is an integer.) The Higgs is a famous example of a scalar.
Paul Dirac - whose eponymous equation involves the first use of spinors in physics - famously wrote in Scientific American that “it is more important to have beauty in one's equations than to have them fit experiment.” Expand this into a main text point
Which is to say, many theoretical physicists who specialize in modern, high energy physics.
Supersymmetry is a mathematical fact, but it is badly broken by our universe. It’s fair to say we have a lot more to learn about how its associated Mathematics best fits into our understanding of Physics.
Phenomenologically, electron repulsion owing to the Pauli Exclusion Principle can be modeled as a traditional, repulsive force. This effective force - modeled loosely by the Lennard-Jones potential, is incredibly strong, approaching 1/r^12 at small distances.
We are glossing over some complexity here. Strictly speaking these facts are true for particles that cannot be distinguished by experiment. That very notion itself is a hold-over from the transition from Quantum Mechanics to Quantum Field Theory which we discussed a bit a few weeks ago:
Using an e isn’t standard practice, but it should work for our purposes.
This is distinct from what we observe in the real world. The photon and the electron are not related in this way. Instead if a† created a photon, we’d expect to find another particle related to the photon, a photino. If e† created an electron, we’d expect to find a scalar particle, often dubbed the selectron. Evidently, supersymmetry - whatever it is - is broken.
The other ψ with a bar over it can be thought of as the positron, the antiparticle partner to the electron.
Actually, since γ carries as space-time vector index μ, it’s a collection of four such matrices packaged at a vector. Quantum Field Theory isn’t terribly hard, but it is full of these technical details. These matrices themselves are intricately related to the ψ. We’ll discuss these in a bonus episode coming soon.
In all likelihood, the particle that would be observed would be a linear combination of other, similar objects. The neutralino was one example that folks were looking for previously.