Angular Momentum is Quantized
Our first look at Spin!
Quantum Mechanics gives a fundamental resolution to angular momentum. It is proportional to Planck's constant, h. After discussing the different kinds of angular momentum, we review how spin angular momentum works, and how we can think about the spin of a microscopic particle like an electron or an atom. We begin the discussion of measuring the spin of such a particle by relating it to its magnetic dipole moment.
As we've seen many times before, Planck's constant - h - sets the scale for Quantum Mechanics. We introduced hh as a finite resolution to the information carrying capacity of space and time. Photons were our first example of this: light waves come in discrete packets of energy, directly proportional to h, and inversely proportional to the wavelength of light, λ:
The constant of proportionality, c, is just the speed of light.
Any information you'd attempt to store or transmit with the electromagnetic field - as you might via fiber optics or photonics - must be coded in terms of photons. Or at least, that's the densest possibly way to package that information. Light with a wavelength λ only exists with integer multiples of E_λ.
Today we'll turn our attention to another way in which h represents a fundamental resolution on information. This time, we'll take the units of h seriously:
The units J⋅s or Joules⋅seconds otherwise known as “energy × time” - are units of angular momentum, a physical property associated with rotational motion.
Angular momentum can be used as a measure of how fast something is spinning - or how fast something like the Earth orbits the sun. Like a photon's energy, Quantum Mechanics also tells us that angular momentum (M) is quantized in integral units proportional to h:
We represent M as a vector because angular momentum typically has an orientation. For the case of a spinning top - or even the Earth - that orientation is aligned with the axis of rotation, and the overall sign is determined by the right hand rule convention.
Particle(s) Spin
Atoms are the building blocks for the world we experience. As we've already seen, atoms have constituent, subatomic particles, like protons and electrons. These are held together by the electromagnetic force, but as we've seen Quantum Mechanics is needed to explain why atoms are stable.
Quantumn Mechanics also tells us that all of these individual particles spin. Protons spin. Electrons spin. When put together into atoms, the whole thing can spin. The electrons can also pick up some extra angular momentum from orbiting the atomic nucleus.
A particle's spin angular momentum is sometimes called intrinsic spin or just spin, because it is always the same for each particle:
Because spin is intrinsic to a species of particle, is common to distinguish between two kinds of angular momentum for microscopic particles: spin [S] and orbital [L]. So that the total angular momentum is given by
Quantum Mechanics predicts what the spin of these individual, subatomic particles should be, as in (1-4). But there's some heavy, technical detail that goes into those predictions. It's a little weird that particles like protons and electrons always spin at exactly the same speed and never slow down. But that's a rule from Quantum Mechanics. Quantum Mechanics also predicts exactly how much orbital angular momentum an electron can have while orbiting the atomic nucleus. The mathematics that describe these predictions also give us a means for combining them together.
At this point, we mention these facts only to observe that they're known. They're under control. We'll learn some of these precise rules as we progress through this course.
Before getting into the details, let's explore what the experiments actually say about a particle's Spin. These experiments open a crucial window into the very heart of Quantum Theory, and so we'll revisit the ideas behind such experiments again and again in what follows.
How to Measure a Particle's Spin
Measuring the spin of macroscopic things is pretty straight forward. The Earth spins literally once a day. The sun helps us measure that. How would you measure the spin of something a bit smaller, like a baseball?
You could use a marker to put a dot on the ball. Then, you could film it rotating, and every time the dot passed through the same point - say the top of the ball - you'd count that as a full rotation. Playing the video, you could write down the timestamp for each rotation. Subtracting each rotation time from the last, you can get a series of measurements for the rotational period of the baseball.
But how can you measure the spin of an electron? You can't mark and electron with a pen. Not only is it too small, if you really think about it, trying to do such a thing doesn't even make sense. To measure an electron's spin, we need something on the electron that we can see spinning.
The Magnetic Dipole Moment
The one thing every electron has is an electric charge. In a manner of speaking, we can see that electric charge spinning. But what would that look like?
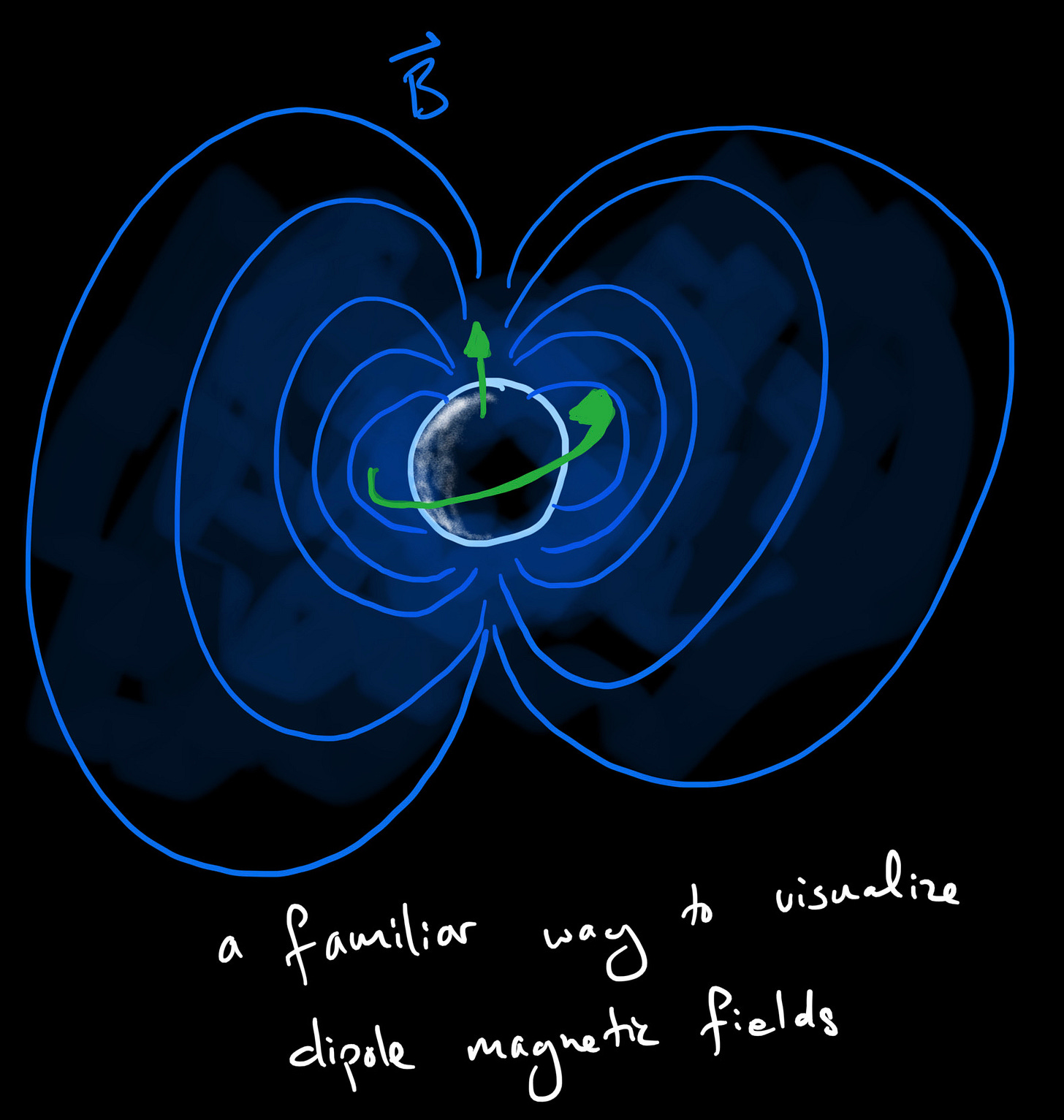
Electric charges generate electric fields just by nature of their existence. That's what causes the oppositely charged protons and electrons to attract each other and bind into atoms. But when electric charges move they also generate magnetic fields. So you might expect a spinning electron to have a tiny magnetic field as well.
Fortunately for us, it does. The proton does too. Lots of particles have tiny magnetic fields. These magnetic fields are directed, like a magnet1 or our Earth, they have a “North” and a “South” pole. It just so happens that a particle's dipole magnetic field b is directly proportional to the spin angular momentum:
This is vector language for saying the the magnitude of the magnetic field is proportional to the magnitude of the spin, and the direction of that magnetic field - the North and South Poles - line up directly with the axis of rotation of that particle2.
In other words, to measure the Spin of an elementary particle, we can measure its dipole magnetic field or magnetic moment, b.
Measuring the Spin of Atoms
While the electric fields of the protons and the electrons essentially cancel each other out3, their magnetic fields don't always cancel. If they combine into atoms in such a way that the atom is spinning, there will be a tiny, residual magnetic field. In other words, the rules for combing a particle's spin are still consistent with (5).
For measuring spin, atoms are easier to work with because they have no net electric field. In a sense we can think of them as individual, tiny bar magnets, floating in space. To measure their spin, we need only expose them to a really big magnetic field. Magnets push on magnets after all, and really big magnets push little magnets the most.
Next time, we'll learn exactly how to use big magnets to measure the atomic spin of silver atoms. The results will reveal something even more surprising the quantization of angular momentum alone.
Exercises
Exercise 1 : (Ampère’s Law)
A crude but useful model for a particle's spin can be devised from elementary electromagnetism. Consider a metal ring of radius R with an electric current i following through it, counterclockwise. Look up Ampère's Law and find the value of the magnetic field in the middle of the ring. For bonus points, find it along the axis of symmetry for the ring, as a function of distance to the middle.
Exercise 2 :
Magnetic fields tend to align. Given Two magnetic fields B_1 and B_2 - perhaps generated by two loops of current as above - the potential energy stored in the collective magnetic field is
where the ⋅ here is the usual vector dot product.
Use this form of U, and the magnetic field you derived in Exercise 1 to argue how the North and South poles of magnets attract and repel each other.
Exercise 3 :
The force from the Magnetic field which pushes on a moving dipole moment can be derived from the potential energy given above. Let the b be the dipole magnetic field associated to an individual atom, and let B be a large, stationary magnet we'll use to measure the spin of that atom. Then (6) becomes,
Generically, a force is given by the gradient of a potential energy, such as U:
Suppose the large magnet had a really sharp point along one direction. Explain how to arrange the big magnet so to make use of this force to deflect a beam of atoms in different directions depending upon the orientation of their dipole moment.
Some Hints for Exercise 3:
Hint 1: What can you say about the derivative of B along the direction with a sharp point?
Hint 2 : Arrange the pointed direction orthogonal to the beam line of individual atoms.
Hint 3 : Don't get caught up with the precise form of b, it's only an atom, so its value is microscopic. The whole point is that B is huge and macroscopic.
In a very real sense, these tiny, atomic magnetic fields in metals like iron all line up to form the magnets we use in daily life. More on this curious fact in a future episode.
A practicing physicist would probably take umbrage with that framing. Just like we can't draw a point on an electron, we can't really define the shape or size of it either. So it doesn't really make sense to define an axis of rotation. In practice, physicists simply treat spin as an inherent property of a particle.
At relatively large distances anyway, distances at which we would measure them.