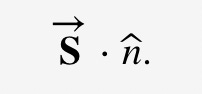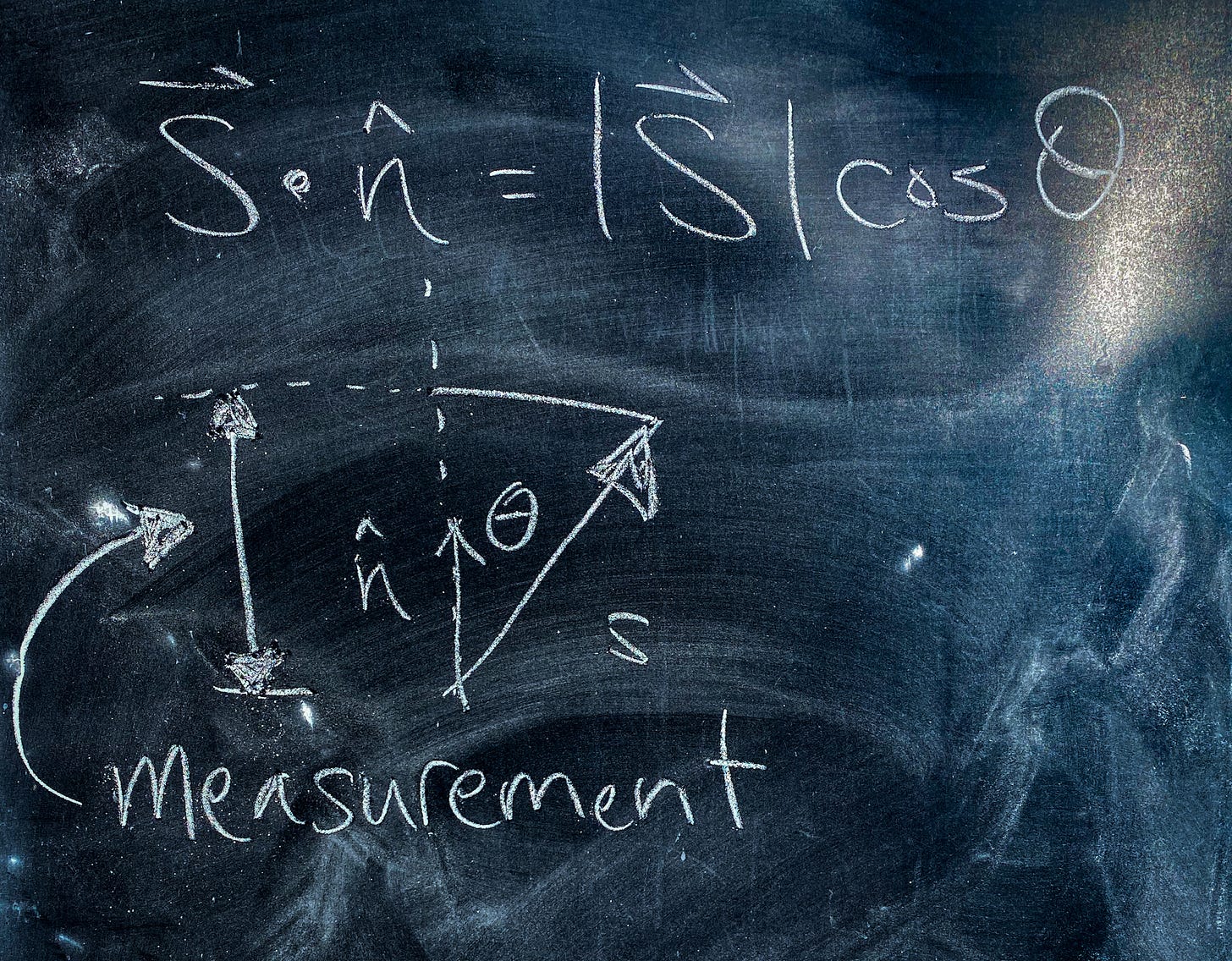Spin as Information

A quick interlude on particle spin

Before diving back into the discussion of the Stern-Gerlach experiment, I realized there might be some confusion about how spin angular momentum is quantized.

We already mentioned that particles like electrons, protons or even atoms spin at an unchanging speed, and that spin must be in integral units of h/4π:

Moreover, individual particle species all share these same precise value of spin, and those precise values will figure importantly in future discussions.

We keep saying that h represents a fundamental resolution to the information carrying capacity of space and time. I wanted to elaborate on this point a little bit.

Spin as a vector

If a particle has a spin angular momentum of S, it must be pointed in some direction. That direction is chosen by axis of spin - which is the same as the axis of symmetry of its magnetic dipole moment. By convention, we chose a positive spin along this axis corresponding to the right hand rule.

Now S can be aligned in any which way. And so can our detector. Importantly, the two do not need to be aligned.

In particular, what actually gets measured is the dot product - the projection of the particle’s spin along the direction of our detector.

Let’s say our detector is set up to measure spin in the direction n. Then the measured value of the particle’s spin should be:

From elementary geometry we know that this is just the magnitude of S times the cosine of the angle - say θ - between S and the detector, n:

At this point, that angle can be anything. It totally depends on the initial particle! So the information we are actually collecting is the value of |S|cosθ.

h and the finite resolution of information

Here’s how the finite resolution of information sneaks in. Here’s how Quantum Mechanics makes things weird. Quantum Mechanics says that you cannot make any just any measurement spin. Even if you measure it at an angle!

If we look at an electron, whose spin is |S|=h/4π, then θ can only be 0 or 180 degrees.

If we look at a photon, whose spin is |S|=h/2π, then θ can be only 0, 90 or 180 degrees.

If we look at a Δ-baryon, with spin |S|=3h/4π, then θ can only be 0, 60, 90 or 180 degrees.

Generally speaking, if the spin of a particle is nh/4π, where n is a nonnegative whole number, then there are n+1 possible values of θ we can measure.

In short:

Particles that spin faster can carry more information!

Now, all this may seem like a weird mishmash of rules that are hard to remember. And it is! Just imagine how the scientists who discovered all this mess felt. But don’t worry. There is an underlying, organizing principle that simplifies all these crazy rules.

Again. I just wanted to share this with you to convince you that I wasn’t lying. h really does set a fundamental resolution for information in space and time. And what I mean by that is, it restricts the set of answers to the kinds of questions you can ask. Just like spin.