Photon Transitions in Hydrogen
Exploring the physics of photons and electrons.
We continue our study of the Hydrogen atom by looking at the specific wavelengths of light it emits. The energies of the individual particles of light - the photons - emitted are then considered in terms of the previously studied product of physical parameters hc.
Last time we explored the constants of nature fundamental Quantum Mechanics: h and c. In particular, we saw that combination give us a characteristic length scale for a given energy:
By comparing this relationship to Coulomb's law of electrostatic force, we noticed that quantum effects became important when the electron was well over 100 nm from the proton. Despite this, observations suggest that the electrons bind to protons at a distance near 0.1 nm. Today we'll explore the relationship between hc and they Hydrogen atom from a slightly different angle.
We’ve also seen that hc determines the resolution of light waves by fixing a discrete number of photons with a minimum energy per wavelength of light:
Today we’ll combine these observations together to catch a first glimpse of how these photons interact with matter.
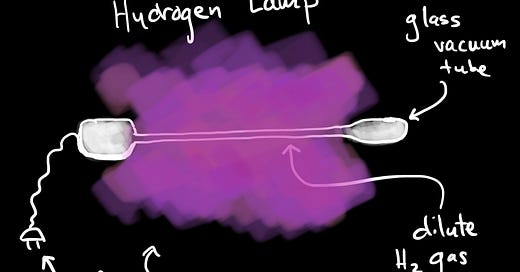
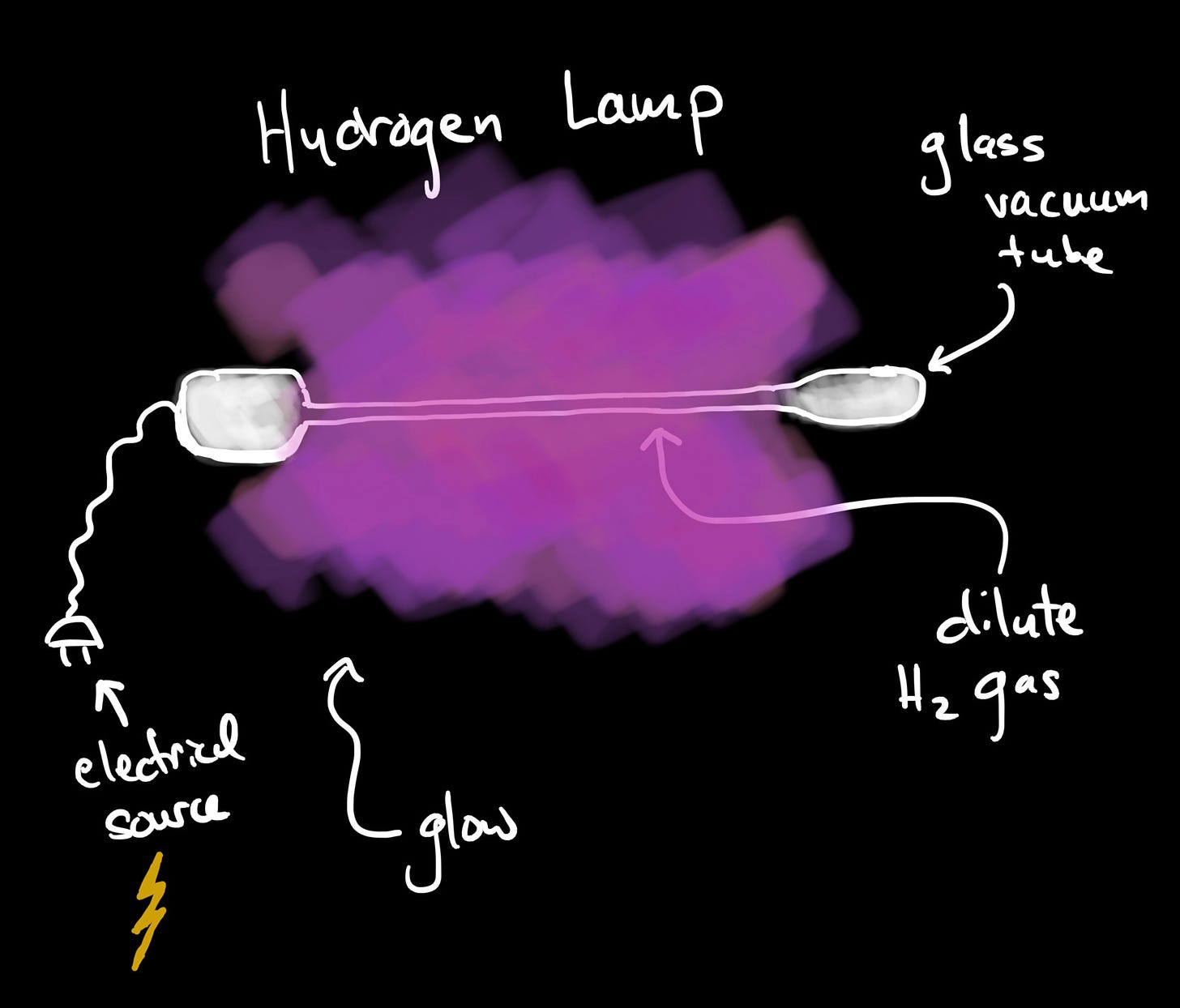
Hydrogen Lamps
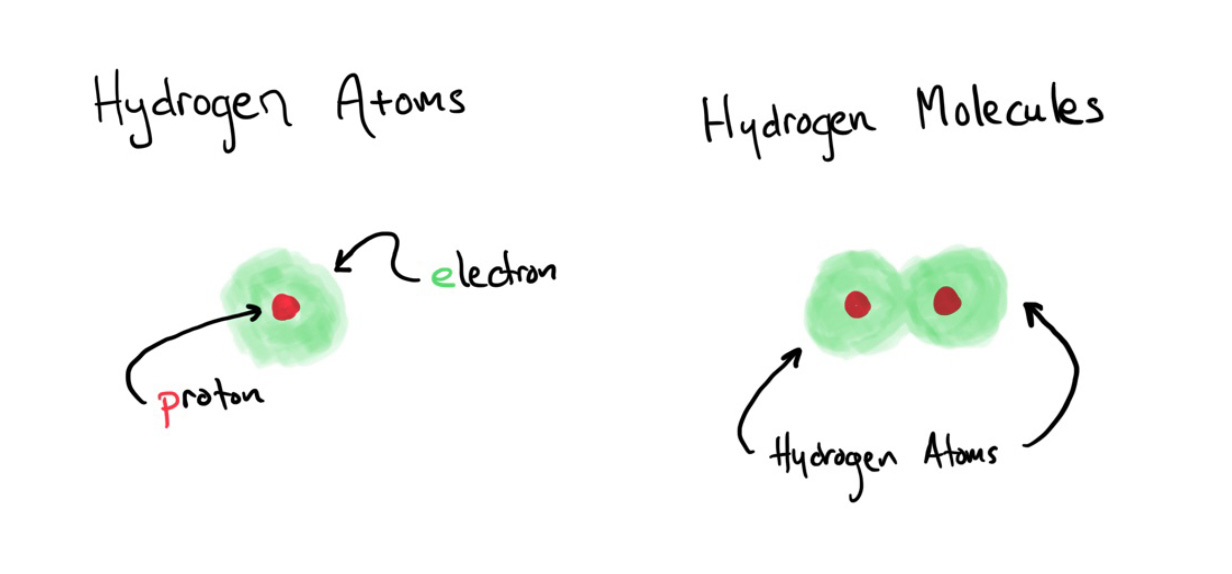
Hydrogen appears in nature as a diatomic gas, meaning it comes in pairs of atoms, with two atoms joined together, H_2. Each atom contributes its own proton and electron.
In low densities, Hydrogen gas can be made into a lamp. Placed in low pressure glass tubes, exposure to electrical current causes the hydrogen gas to glow. The electric current energizes the electrons. They gain enough energy to break the diatomic bond, but not enough energy to escape the Coulomb force that binds them into atoms. They do, however, gain enough energy to reach a higher orbit. The current gives them more potential energy.
As the electrons fall back down to a lower energy, they emit particles of light or photons. In aggregate, those photons constitute the light of the lamp.
We’ve already seen that the energy of an emitted photon of wavelength λ is given by the relationship
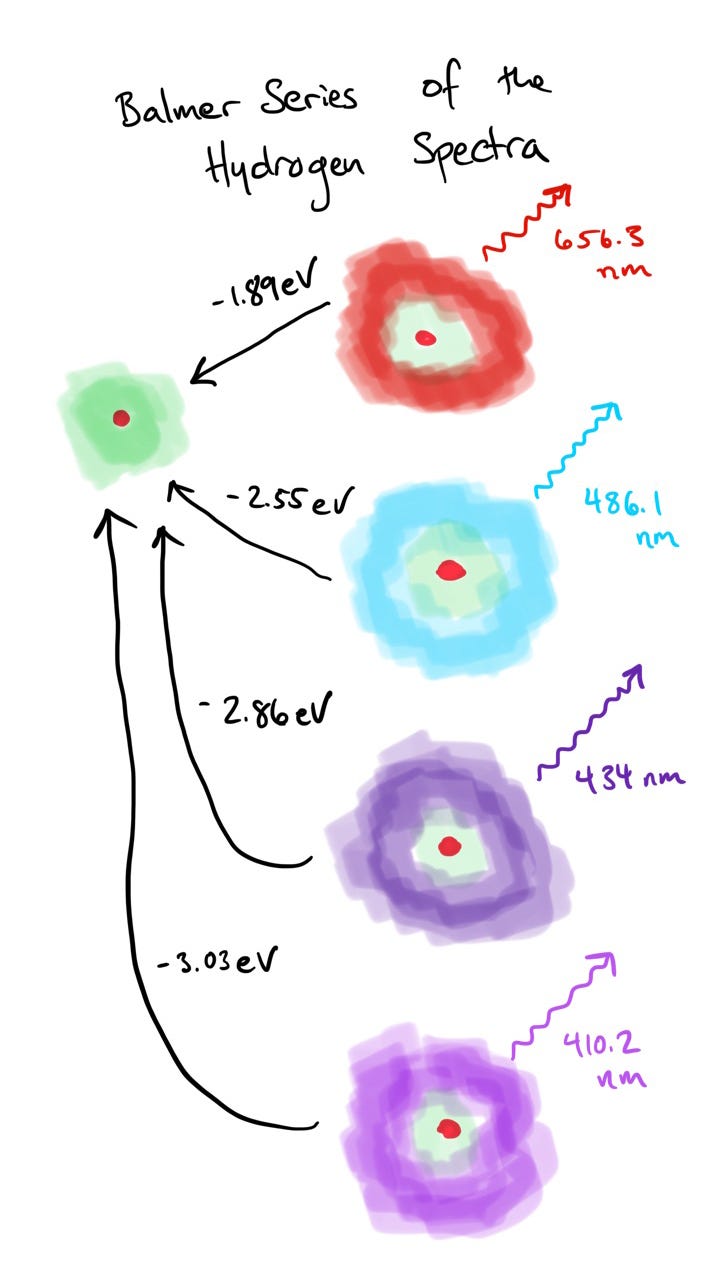
The Balmer Series
What perplexed physicists near the turn of the 20th century was the properties of the light emitted by Hydrogen. When passed through a prism, the light split not into a rainbow, but into four, distinct colors at four, very specific wavelengths. This series of four colors has come to be known as the Balmer Series:
RED : 656.3 nm : energy emitted 1.89 eV
CYAN : 486.1 nm : energy emitted 2.55 eV
BLUE-VIOLET : 434.0 nm : energy emitted 2.86 eV
VIOLET : 410.2 nm : energy emitted 3.03 eV
We now understand this discrete series of colors emitted by Hydrogen lamplight to be related to discrete or quantized energy levels of the electron in a Hydrogen atom. That is, the electrons in the atom can only exist in specific “orbits” or “energy levels”. When they drop between levels, they lose a specific amount of energy. That energy is carried away by the emission of a photon of corresponding energy.
We'll explore some of the associated quantitative details in the exercises below.
Exercises
Exercise 1 : Show by explicit investigation that the energy difference for the transition between different energy levels of the electrons in hydrogen are given by the formula:
where n is a positive, whole number greater than 2 and E is a constant. Find the explicit value of that constant E.
Exercise 2 : Compute the first three, positive energy differences for each of the similar formulae
Use the formula (1) to find the associated wavelength of the light emitted by these transitions. Why can’t we see those lines in our hydrogen lamp?