Lagrange Points and other Curious Orbits
Space rocks of all shapes and sizes enjoy all kinds of wild orbits.
Howdy!
After last week’s piece about the James Webb Space Telescope, there were a few questions about “Lagrange Points”: those points in space where the Sun and Earth’s gravity “cancel each other out”. Today we’ll add a bit more color and texture to their discussion.
Please do keep those questions coming!
Sean
The Demotion of Pluto
In January of 2005, the planet-like object Eris was discovered orbiting the sun. At the time, it appeared to be bigger that Pluto, and was much further out in space. Not two months later, Makemake was found. Astronomers quickly realized that Pluto wasn’t special, and there are probably many objects like it out beyond Neptune.
When the dust settled, Pluto was demoted to “dwarf planet”.
That process of “demotion” required the IAU to define what a planet was. One major plank of that definition demands that a planet “clear its orbit” from similar sized objects. Clearing the orbit means aggregating moons and otherwise tossing out other objects. Like so many objects out near the edge of our solar system, Pluto, evidently, failed to live up to these requirements.
The armchair blowback to this decision was understandable, but a moment to educate the public was missed. There are a lot of objects in our solar system, of all kinds of shapes and sizes, and that diversity should be celebrated!
The World isn’t Flat, but its Orbit Is
Gravity is universal. All matter attracts other matter. How strong that attraction is depends on two things: how much matter there is, and how close it is together.
Orbits are a byproduct of this universal law. The moon orbits the Earth. The Earth orbits the Sun. The Sun orbits Sagittarius A*, a supermassive black hole in our galaxy’s center, taking us all along with it. Our galaxy even has its own satellite galaxies. Notable examples glow in the Southern skies: the Magellanic Clouds.
In all these cases, the orbits are the standard, planar ones. Like the hands of a clock, a planet like the Earth moves around in a flat, two-dimensional plane. This is a special property of like gravity and electricity.
Now given a bunch of different orbits - like a solar system full of planets - all these planes could be different. It’s remarkable that our solar system is fairly organized. Coplanar. Flat.
Coplanar except for the eccentric and out-of-plane orbits of objects like Pluto, Eris and Makemake. Individually, their orbits lie flat in a single plane, but the angle at which they orbit relative to the other plants is wonky.
But even these outliers seem orderly compared to other objects in the solar system.
Lagrange Points
Given that gravity pulls everything together, you might wonder if you could be trapped between the pull of two objects. Is there a place between the Sun and the Earth where the force of gravity just cancels out?
Indeed, there is.
Given two big, celestial objects, like the Earth and the moon, there are five such places. They’re called Lagrange Points, and they follow the planar orbit of the smaller of the pair, much like a “peace” sign.
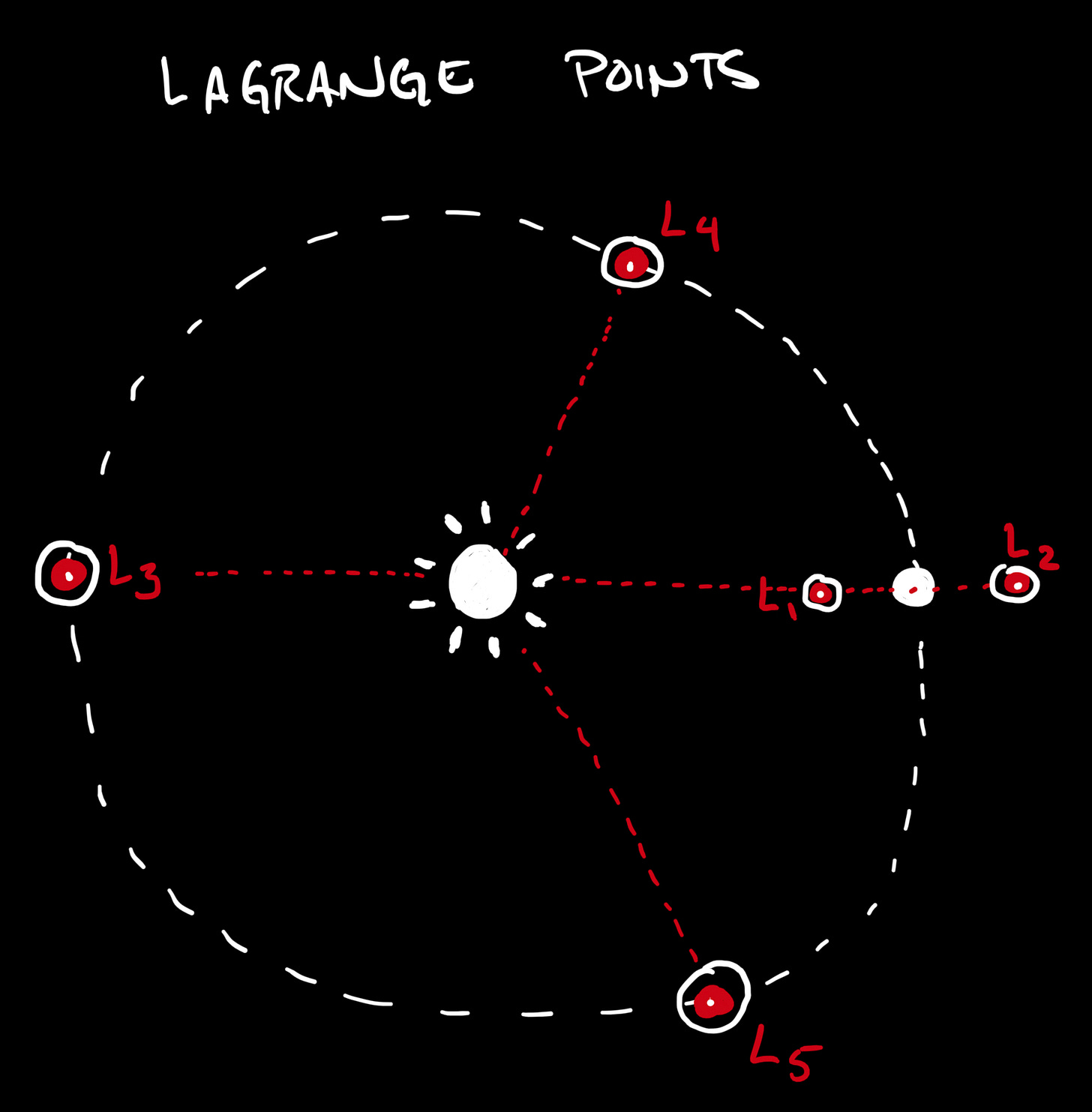
Traditionally, each point is called “Ln” where n labels the points, 1 to 5.
L1 lies between the two bodies, and L2 lies opposite the smaller body. L3 lies out on the opposite side of the orbit. L4 leads the orbit of the smaller object, and L5 lags behind it.
Famously. L2 - behind the Earth - is where the James Webb Space Telescope now resides.
Like dolphins or birds riding in the wake of a large boat, objects can hitch a ride around any of those five points. They will fall into something of an “orbit” around them, although anything orbiting L1, L2 or L3 is technically unstable. Like a gentle slope of an unleveled table, it doesn’t take much for such objects to fall out of orbit.
Orbits around L4 and L5 are dynamically stabilized by the Coriolis Effect - a three-dimensional version of centripetal acceleration you feel while driving through turns too quickly.
All of these orbits, stable or not, deserve scrutiny. They’re not planar orbits like the planets and stars enjoy. Rather, they tend to form wild, three dimensional shapes, like tadpole orbits or the geometrically pleasing Lissajous Orbits.

Lagrange Points add considerable character to the types of “orbits” available to celestial bodies.
The Greeks and the Trojans
Because L4 and L5 are stable orbits, you might expect objects to aggregate around them. This is indeed the case. Generically, such objects are called “Trojans”.
The astroid belt is a ring of debris between Mars and Jupiter that contains rocks of all sizes - including some dwarf planets. These are not the only asteroids in the solar system.
The L4 and L5 points of Jupiter’s orbit also contains astroids. Based on observations, it is possible they contain about as many as in the astroid belt itself. Historically, L4 asteroids have been named after Greek heroes of the Trojan War, and L5 have been named after the Trojans.
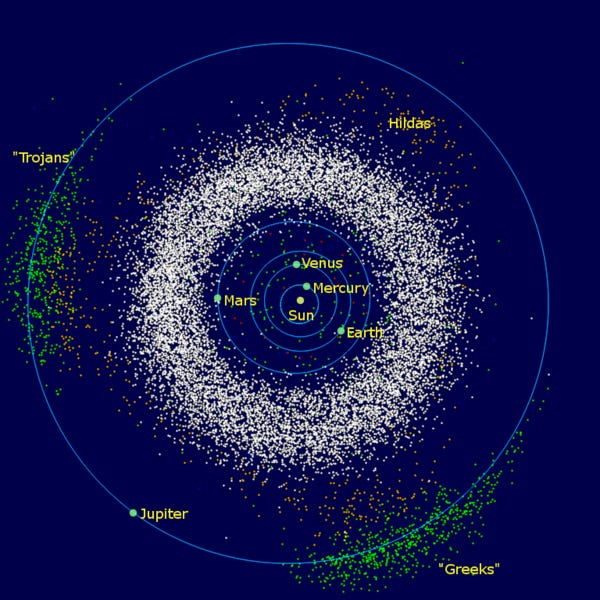
Although there are a few labeling errors.
Confusingly, the largest of these, 624 Hektor (named for the Trojan Hero), lies as a “spy” in the Greek camp at L4. Based on observations from the Keck Observatory, 624 Hektor is believed to be a pair of very closely orbiting asteroids. Amusingly, 624 Hektor also has a moon!
Jupiter may have “cleared its orbit” of planet-sized objects, but there is a lot of diversity amongst the rocks in its wake.
Earth Trojans
Given Jupiter’s cache of space rocks, you might want if other Lagrange points - say those around the Earth - host them too.
Again. Yes. Yes they do.
The Earth-Sun L4 point hosts two known large trojan asteroids. 2010 TK7 and 2020 XL5. Both objects have diameters that measure in the 100s of meters, and both objects enjoy highly eccentric “tadpole” orbits, which can be thought of as elongated loops that not only go around the L4 point between the Earth and the Sun, but also oscillate back and forth along the Earth’s main orbital path.
Precision measurements of 2010 TK7’s “tadpole” orbit have suggested a particularly wild history, possibly “jumping” from L5 to L4 via an unstable L3 to its current orbit.
Some Finer Points
Even with Newton’s Law of universal gravitation, planar orbits aren’t easy to compute from scratch. There are still plenty of algebraic tricks involved. It’s an excellent case study for students with a year or two of calculus under their belt.
By comparison, the general problem of three mutually attracting objects is completely intractable. Progress is incremental, but some fascinating special cases have been studied.
Joseph-Louis Lagrange - the mathematician who initiated the study of those eponymous points - lived in the 18th century. Since then, these points have moved from mathematical curiosity to science fiction to repeated bouts of practical, scientific application.
To describe the details, we’ll refer to these objects as the Sun, the Earth and some relatively tiny space rock orbiting the Sun-Earth Lagrange points.
The Details
The stability of a small object orbiting a Lagrange points depends on some assumptions about the size of the three objects. In particular, to acquire Trojans, the L4 and L5 points about the Sun and the Earth must be stable. This happens only if the mass ratio of the Sun to its planet is about 25.
The rate at which the unstable orbits around L1, L2 and L3 unwind depends primarily on the rate at which the Earth orbits the Sun. Very roughly, the space rock will stay close to these Lagrange points for about a year. For a similar object between the Earth and the Moon, it would be about a month.
Actually, there is a notable correction to this - a percentage based on the the square root of the ratio of the mass of the Sun to the Earth. For a tiny space rock, that means it would have only few months before it falls away.
With ever more objects being lifted into space - and the ever-present objective hazard of massive space rocks - the study of near earth objects remains an important, practical application of these kinds of classical astrophysics today. As a byproduct of this serious work, we get to enjoy observing this wild zoo of solar system objects and their orbital dynamics.



